工欲善其事,必先利其器。学习逻辑回归之前,肯定要对现行回归有所了解
线性回归
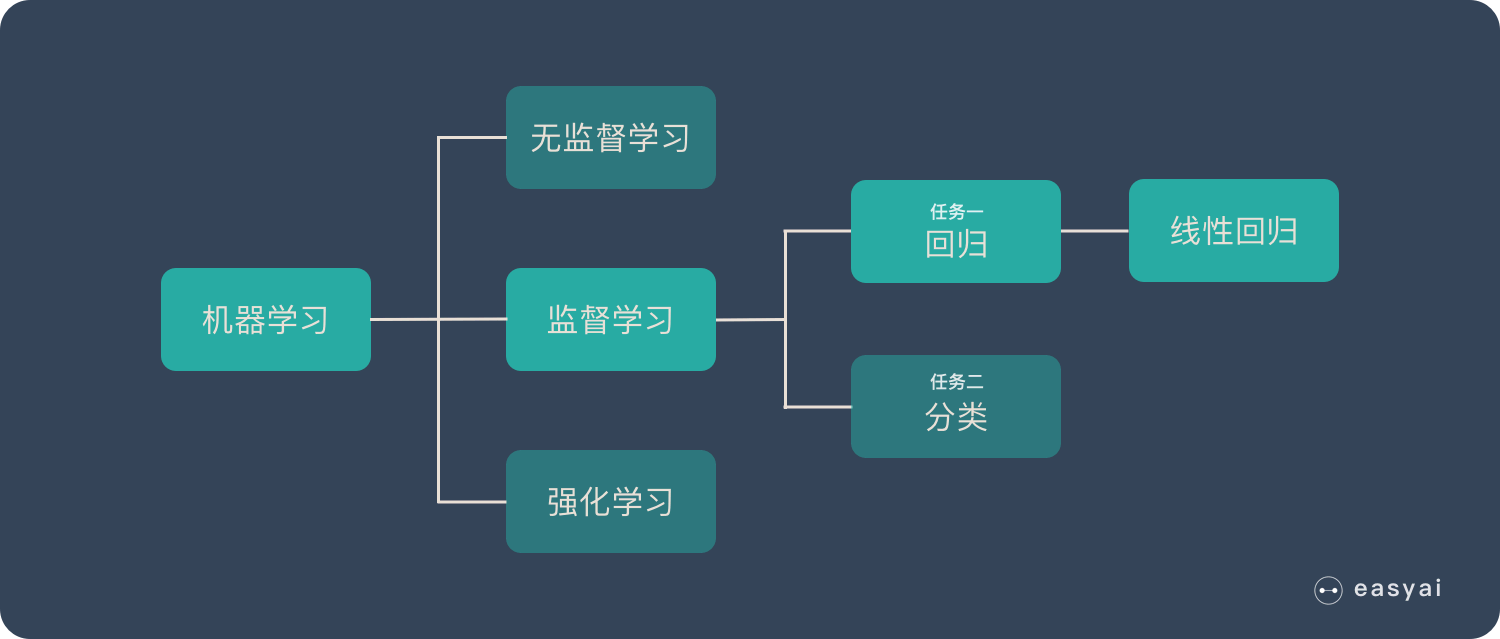
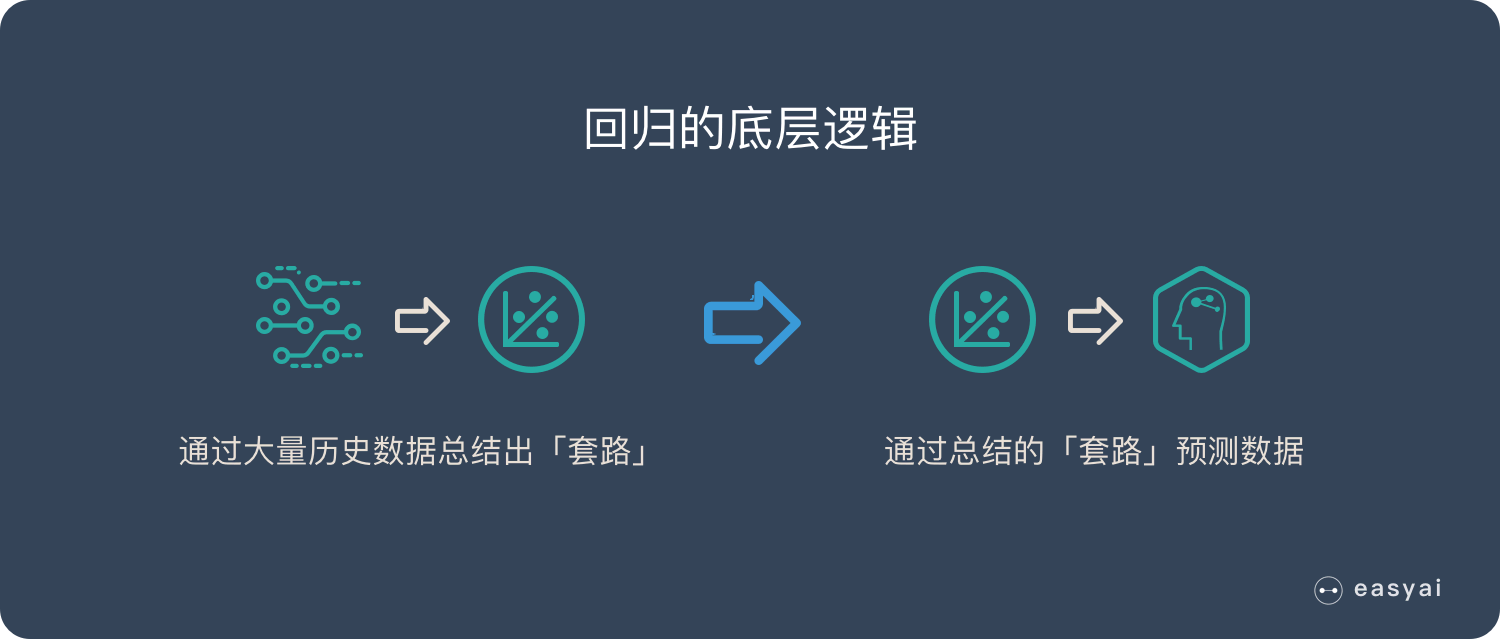
回归的原理
什么是线性
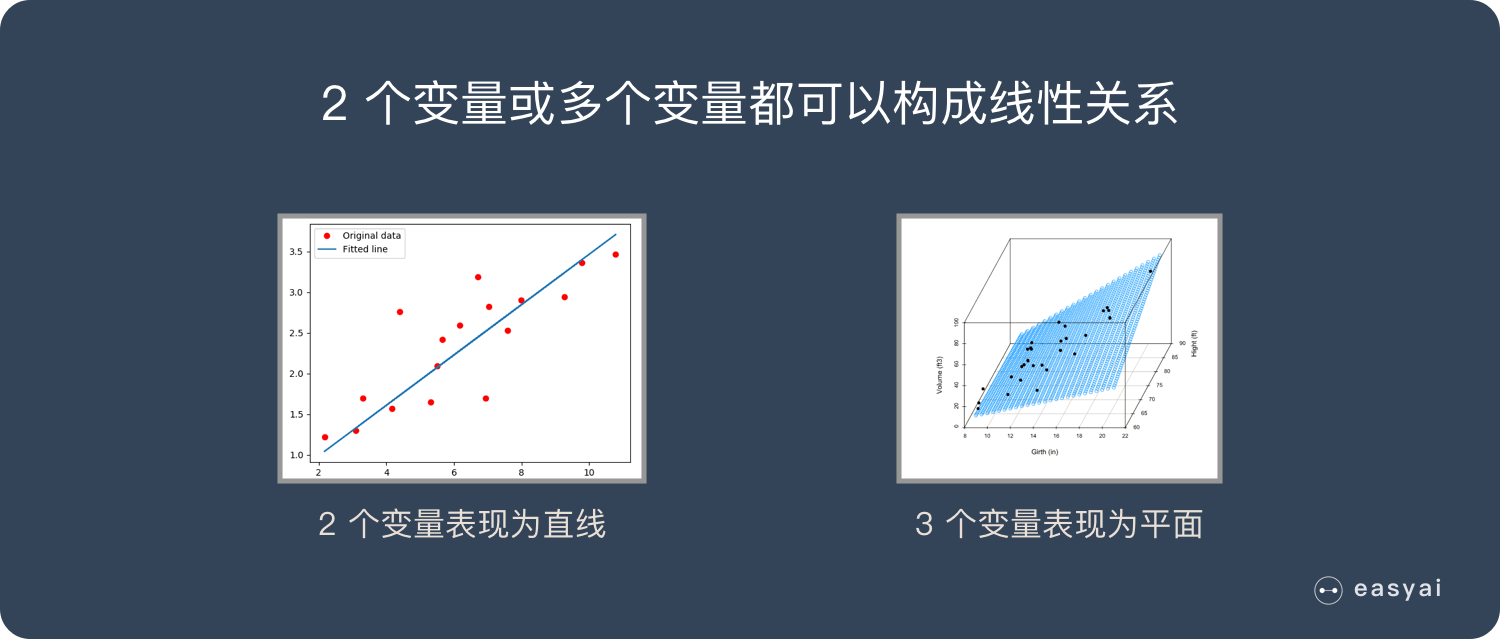
什么是线性回归

线性回归优缺点

逻辑回归的由来
因为我们的线性模型只能去拟合数据的发展趋势(递增或递减),并不适合做分类任务,所以引入了sigmoid函数将线性回归压缩至0~1之间,产生概率值,达到可以解决我们日常生活中一些分类的问题
罗辑回归


案例
- 一封邮件是垃圾邮件的肯能性(是、不是)
- 你购买一件商品的可能性(买、不买)
- 广告被点击的可能性(点、不点)
优点
- 实现简单,广泛的应用于工业问题上;
- 分类时计算量非常小,速度很快,存储资源低;
- 便利的观测样本概率分数;
- 对逻辑回归而言,多重共线性并不是问题,它可以结合L2正则化来解决该问题;
- 计算代价不高,易于理解和实现;
缺点
- 当特征空间很大时,逻辑回归的性能不是很好;
- 容易欠拟合,一般准确度不太高
- 不能很好地处理大量多类特征或变量;
- 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分;
- 对于非线性特征,需要进行转换;
公式
逻辑函数中是引入了线性回归的公式,所以我们要从线性回归开始推导我们的公式
$y_i=W_0+W_1X_1+b_i,\ i=1,\dots,n.$
引入矩阵的概念呢我们的公式就简化为 $y=w^Tx+b$
逻辑函数公式为 $\frac { 1 } { 1 + e ^ { -z }}$
根据导数公式
$y=\frac{1}{x^n}$
$y’=-\frac{n}{x^{n+1}}$
逻辑回归的单模型只能适用于二分类问题,那我们的实际输出只有0和1所以
$p(y=1|x,w)=\frac{1}{1+e^{-w^Tx+b}}$
$p(y=0|x,w)=\frac{e^{-WTx+b}}{1+e^{-w^Tx+b}}$
$p(y|x,w)=p(y=1|x,w)^y[1-p(y=0|x,w)]^{1-y}$
目标函数为
$W_{MLE},B_{MLE}=argmax_{w,b}(\prod\limits_{i=1}^nP(y_i|x_i, w,b))$
为了计算机方便计算引入log并替换乘法为加法 防止underflow(太长),overflow(太大)带入公式可以表达成
$W_{MLE},B_{MLE}=argmax_{w,b}(\sum\limits_{i=1}^nlogP(y_i|x_i, w,b))$
最大转最小
$W_{MLE},B_{MLE}=argmin_{w,b}(-\sum\limits_{i=1}^nlogP(y_i|x_i, w,b))$
$p(y|x,w)=p(y=1|x,w)^y[1-p(y=0|x,w)]^{1-y}$ 公式转换为 $-\sum\limits_{i = 1}^{n}y_ilogP(y_i|x_i,w,b)+(1-y)log[1-P(y_i|x_i,w,b)]$
逻辑回归的梯度下降
对W求导
$-\sum\limits_{i = 1}^{n}y_ilog(\sigma(w^Tx+b))+(1-y_i)(log(1-\sigma(w^Tx+b)))$
$-\sum\limits_{i=1}^ny_i\frac{\sigma(w^Tx+b)(1-\sigma(w^Tx+b))}{\sigma(w^Tx+b)}x_i+(1-y_i)\frac{-\sigma(w^Tx+b)(1-\sigma(w^Tx+b))}{1-\sigma(w^Tx+b)}x_i$
$-\sum\limits_{i=1}^ny_i(1-\sigma(w^Tx+b))x_i+(y_i-1)\sigma(w^Tx+b)x_i$
$-\sum\limits_{i=1}^ny_i-\sigma(w^Tx+b)x_i$
$\sum\limits_{i=1}^n(\sigma(w^Tx+b)-y_i)x_i$
对B求导 结果少了一个$x_i$
$\sum\limits_{i=1}^n(\sigma(w^Tx+b)-y_i)$
因为考虑到求和公式,所以这里考虑的是所有样本, 当数据量很大的时候效率很低
随机梯度下降
随机梯度下降不考虑求和,考虑的是每个样本
for iter=1 … 收敛:
shuffle(sample)
for i=1 … n
W_new = W_old - 学习率 * $[\sigma(w^Tx+b)-y_i]x_i$
b_new = b_old - 学习率 * $\sigma(w^Tx+b)-y_i$
mini-batch 梯度下降
SGD和SD的折中方案
for iter=1… 收敛:
mini-batch = sample(batch_data)
W_new = W_old - 学习率 * $\sum\limits_{i \in mini-batch}^n[\sigma(w^Tx+b)-y_i]x_i$
b_new = b_old - 学习率 * $\sum\limits_{i \in mini-batch}^n(\sigma(w^Tx+b)-y_i)$
梯度下降的区别
梯度下降很稳定,SGD某个样本可能有噪声,不是很稳定 学习率设置低一些,mini-batch折中一下




